22.10.2025
Материал подготовлен на примере технологии 1С:Элемент. Все примеры выполнены на языке 1С:Элемент, который используется в среде разработки "1С:Предприятие.Скрипт". Среду можно бесплатно скачать с официального сайта lang.1c.ru. Приведённые подходы к оценке сложности алгоритмов могут быть полезны и разработчикам решений на платформе 1С:Предприятие.
Почти всегда существует способ проще и лучше, чем тот, что первым пришёл вам в голову. — Дональд Кнут
В мире разработки редко кто спорит о важности чистого кода, архитектуры и тестов. Но один из самых фундаментальных аспектов инженерного мышления нередко оказывается в тени — анализ сложности алгоритмов. Это не теоретическая абстракция, а практический инструмент, который помогает понять, насколько хорошо масштабируется ваш код, как он поведёт себя при увеличении объёма данных, и где возникают узкие места.
Понимание сложности — это умение видеть не только, как работает алгоритм, но и как он ведёт себя в динамике. И если сегодня ваш код обрабатывает тысячи записей, а завтра — миллионы, именно анализ сложности определит, выдержит ли он этот рост, и не будет ли в результате замедления.
Когда мы говорим об эффективности алгоритма, мы обычно имеем в виду две вещи:
Обе метрики описывают не конкретные секунды или мегабайты, а зависимость от масштаба задачи. Это принципиально важно: мы не меряем скорость на конкретной машине, а анализируем поведение в пределе.
Чтобы описывать эту зависимость, используется асимптотическая нотация, чаще всего — Big O.
Формально, запись O(f(n)) означает, что время выполнения алгоритма растёт не быстрее, чем функция f(n) при больших n. Т.е. описывает верхнюю границу.
Другими словами, Big O — это способ сказать: «если входные данные станут в 10 раз больше, насколько медленнее станет алгоритм».
Мы игнорируем конкретные коэффициенты и фокусируемся на темпе роста, потому что именно он определяет масштабируемость.
Сложность алгоритма может отличаться в зависимости от входных данных. Например, поиск элемента в отсортированном массиве может закончиться за одну операцию — или пройти весь массив. Поэтому различают:
Именно худший случай чаще используется при анализе: он даёт верхнюю границу, обеспечивая предсказуемость.
Когда мы говорим, что операция выполняется за константное время, мы имеем в виду, что её длительность не зависит от размера входных данных.
Сколько бы элементов ни содержал массив, время выполнения операции получения элемента остаётся одинаковым.
Чтобы увидеть это на практике, достаточно взглянуть на простой эксперимент:
Копировать в буфер обменаметод Скрипт() КонстантнаяCложность() ; метод КонстантнаяCложность() знч Массив100 = ПолучитьМассивСлучайныхЧисел(10000) знч Массив10000 = ПолучитьМассивСлучайныхЧисел(1000000) пер НачалоОперации = ДатаВремя.Сейчас() Массив100.Получить(50) пер ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время доступа к элементу по индексу в массиве из 100 элементов: %{ДлительностьОперации} мс") НачалоОперации = ДатаВремя.Сейчас() Массив10000.Получить(5000) ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время доступа к элементу по индексу в массиве из 10 000 элементов: %{ДлительностьОперации} мс") ;
Результат эксперимента:
Время доступа к элементу по индексу в массиве из 100 элементов: 1 мс
Время доступа к элементу по индексу в массиве из 10 000 элементов: 1 мс
Несмотря на то, что один массив в 100 раз больше другого, время доступа к элементу практически не изменилось. Это и есть поведение константной сложности.
Что это значит на уровне модели?
Операция доступа по индексу (Массив.Получить(i)) в большинстве реализаций выполняется одинаково быстро, потому что:
Процессор делает одно и то же количество шагов, независимо от размера массива.
Даже если массив состоит из миллиона элементов, вычисление позиции для 5000-го занимает те же наносекунды, что и для 5-го.
Важно понимать: O(1) не означает мгновенно. Это значит лишь, что время выполнения не растёт с увеличением n.
Операция может занимать 1 мс, 10 мс или даже секунду — но если она всегда занимает примерно одинаковое время, это всё ещё O(1).
Например, вызов кэшированной функции может быть O(1), но при этом медленным из-за задержек сети или ввода-вывода.
А вот поиск элемента в массиве без индексации, наоборот, будет O(n), даже если на малых данных кажется «почти мгновенным».
Где встречается константная сложность
Типичные операции O(1) включают:
Константная сложность — это строительный кирпич эффективных алгоритмов.
Она сама по себе не гарантирует скорость всей программы, но если вы добились того, чтобы большинство критических операций выполнялись за O(1), значит, ваш код масштабируется предсказуемо и стабильно.
Константная сложность — это не просто «быстро», это устойчиво.
Алгоритм с O(1) временем ведёт себя одинаково при 10 элементах и при миллионе.
И именно эта предсказуемость делает его базовым эталоном эффективности, на который равняются все остальные классы сложности.
Если константная сложность (O(1)) — это «независимо от размера данных», то линейная сложность (O(n)) означает, что время выполнения растёт прямо пропорционально количеству элементов.
Каждый элемент обрабатывается хотя бы один раз, и общее время выполнения увеличивается вместе с объёмом входных данных.
Рассмотрим простой пример, который демонстрирует линейное поведение:
Копировать в буфер обмена
метод Скрипт() ЛинейнаяCложность() ; метод ЛинейнаяCложность() знч Массив100000 = ПолучитьМассивСлучайныхЧисел(100000) знч Массив10000000 = ПолучитьМассивСлучайныхЧисел(10000000) пер НачалоОперации = ДатаВремя.Сейчас() пер СуммаЭлементов = ПолучитьСуммуЭлементовМассива(Массив100000) пер ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время вычисления массив 100 000 элементов: %{ДлительностьОперации} мс. Результат: %{СуммаЭлементов}") НачалоОперации = ДатаВремя.Сейчас() СуммаЭлементов = ПолучитьСуммуЭлементовМассива(Массив10000000) ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время вычисления массив 10 000 000 элементов: %{ДлительностьОперации} мс. Результат: %{СуммаЭлементов}") ; метод ПолучитьСуммуЭлементовМассива(МассивЧисел: Массив): Число пер СуммаЭлементов = 0 для Элемент из МассивЧисел СуммаЭлементов += Элемент ; возврат СуммаЭлементов ;
Результат выполнения:
Время вычисления массив 100 000 элементов: 12 мс. Сумма всех элементов: 4996734023
Время вычисления массив 10 000 000 элементов: 651 мс. Сумма всех элементов: 499983640264
Рост объёма данных примерно в 100 раз приводит к увеличению времени выполнения примерно в 50–60 раз (что близко к линейной зависимости с поправкой на накладные расходы системы).
Функция ПолучитьСуммуЭлементовМассива() проходит по каждому элементу массива ровно один раз, выполняя одно и то же простое действие — сложение.
Если элементов в массиве становится в два раза больше, то и сложений выполняется в два раза больше.
Формально это можно записать как:
T(n) = c * n
где c — это время на обработку одного элемента, а n — количество элементов.
Константа c зависит от конкретного оборудования и реализации, но сама зависимость линейна.
Алгоритмы с O(n) — это рабочие лошадки любой системы.
Они не идеальны, но надёжны и предсказуемы.
Типичные примеры:
Такие алгоритмы масштабируются достаточно хорошо:
увеличение объёма данных в 10 раз увеличивает время работы примерно в 10 раз — никаких сюрпризов.
Иногда можно услышать: «O(n) — это нормально, значит быстро». Не всегда.
Если n — это десятки или сотни миллионов записей, даже линейный проход займёт секунды или минуты.
Здесь важно помнить, что асимптотика описывает характер роста, но не абсолютное время.
Кроме того, иногда линейные операции встраиваются друг в друга, создавая эффект O(n?) — например, когда для каждого элемента выполняется ещё один линейный поиск.
Линейная сложность — это золотая середина между простотой и масштабируемостью.
Алгоритмы O(n) легко читать, легко прогнозировать и, при разумных размерах данных, дают приемлемую производительность.
Но важно помнить: каждая операция на каждом элементе имеет свою цену — и в больших системах именно сумма этих «маленьких» действий определяет скорость всего приложения.
Когда говорят, что алгоритм «масштабируется хорошо», чаще всего имеют в виду именно линейно-логарифмическую сложность.
Это разумный компромисс между скоростью и универсальностью. Такие алгоритмы растут немного быстрее линейных, но всё ещё намного медленнее квадратичных, что делает их эффективными при работе с большими объёмами данных. Типичный представитель этого класса — сортировка слиянием (Merge Sort).
Приведённый ниже пример демонстрирует работу алгоритма слияния и рекурсивного разбиения массива:
Копировать в буфер обменаметод Слить(ЛевыйМассив: Массив<Число>, ПравыйМассив: Массив<Число>): Массив<Число> знч Результат = <Число>[] пер ИндексЛевый = 0 пер ИндексПравый = 0 // Проходим оба массива, пока оба не закончились пока (ИндексЛевый < ЛевыйМассив.Размер() и ИндексПравый < ПравыйМассив.Размер()) если (ЛевыйМассив[ИндексЛевый] <= ПравыйМассив[ИндексПравый]) Результат.Добавить(ЛевыйМассив[ИндексЛевый]) ИндексЛевый += 1 иначе Результат.Добавить(ПравыйМассив[ИндексПравый]) ИндексПравый += 1 ; ; // Добавляем оставшиеся элементы левого массива пока (ИндексЛевый < ЛевыйМассив.Размер()) Результат.Добавить(ЛевыйМассив[ИндексЛевый]) ИндексЛевый += 1 ; // Добавляем оставшиеся элементы правого массива пока (ИндексПравый < ПравыйМассив.Размер()) Результат.Добавить(ПравыйМассив[ИндексПравый]) ИндексПравый += 1 ; возврат Результат ; // Рекурсивная функция сортировки слиянием метод СортировкаСлиянием(ИсходныйМассив: Массив<Число>): Массив<Число> если (ИсходныйМассив.Размер() <= 1) возврат ИсходныйМассив ; пер СерединаМассива = (ИсходныйМассив.Размер() / 2).ЦелаяЧасть() знч ЛевыйМассив = СортировкаСлиянием(ИсходныйМассив.ПодМассив(0, СерединаМассива)) знч ПравыйМассив = СортировкаСлиянием(ИсходныйМассив.ПодМассив(СерединаМассива)) возврат Слить(ЛевыйМассив, ПравыйМассив) ; метод Скрипт() пер НачалоОперации = ДатаВремя.Сейчас() знч ИсходныйМассив10 = ПолучитьМассивСлучайныхЧисел(10) знч ОтсортированныйМассив10 = СортировкаСлиянием(ИсходныйМассив10) пер ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Отсортированный массив: %ОтсортированныйМассив10") Консоль.Записать("Длительность: %ДлительностьОперации мс") НачалоОперации = ДатаВремя.Сейчас() знч ИсходныйМассив1000 = ПолучитьМассивСлучайныхЧисел(1000) знч ОтсортированныйМассив1000 = СортировкаСлиянием(ИсходныйМассив1000) ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Отсортированный массив: %{ОтсортированныйМассив1000.Представление().Обрезать(50,"...]")}") Консоль.Записать("Длительность: %ДлительностьОперации мс") ;
Результат выполнения:
Отсортированный массив: [320, 1794, 1853, 2173, 2796, 5968, 6504, 8968, 9516, 9993], Длительность: 6 мс
Отсортированный массив: [7, 13, 20, 24, 35, 35, 36, 73, 85, 89, 93, 97...], Длительность: 46 мс
Даже при увеличении размера массива в 100 раз, время выросло меньше чем в 10 раз — поведение, характерное именно для O(n log n).
Сортировка слиянием (merge sort) основана на двух идеях:
На каждом уровне рекурсии мы выполняем линейный проход по данным (O(n)), а число уровней разбиений составляет log?(n) — потому что на каждом шаге массив делится пополам.
В результате получаем общую формулу:
T(n) = n ? log?(n)
На первый взгляд, log n — незначительная добавка, но разница колоссальная.
Например:
Разница — в сотни раз.
Поэтому O(n log n) — это реалистический предел скорости для алгоритмов сортировки на основе сравнений (merge sort, quick sort, heap sort и др.).
Каждое слияние (Слить()) само по себе работает за O(n) — оно просто проходит по обоим массивам, добавляя элементы по порядку.
Но из-за рекурсивного деления мы выполняем такие слияния на каждом уровне дерева вызовов:
Если сложить все уровни, общее количество операций даёт n ? log n.
Сортировка слиянием требует дополнительной памяти для хранения временных массивов (результатов слияний).
Поэтому пространственная сложность — O(n).
Это одна из причин, почему на практике иногда выбирают другой алгоритм сортировки - QuickSort: он тоже O(n log n), но может работать почти без дополнительной памяти.
O(n log n) — это оптимум для большинства реальных задач, где требуется упорядочивание, группировка или сведение данных.
Линейные алгоритмы быстрее, но они применимы только к уже отсортированным структурам.
А всё, что медленнее O(n log n), быстро перестаёт быть применимым при больших объёмах.
Существует доказательство, что ни один алгоритм сортировки на основе сравнений не может быть быстрее O(n log n) в худшем случае. Это связано с количеством возможных перестановок и структурой бинарного дерева решений.
Чтобы обойти этот предел, нужно изменить саму модель — например, использовать не сравнения, а разрядный анализ (как в radix sort), что возможно не для всех типов данных.
Линейно-логарифмическая сложность — это компромисс между вычислительными затратами и гибкостью применения.
Она отражает идею «делить и властвовать»: уменьшать задачу на каждом шаге, сохраняя общее количество операций разумным.
Сортировка слиянием — классический пример того, как инженерная элегантность превращается в асимптотическую эффективность.
Квадратичная сложность означает, что количество операций растёт пропорционально квадрату размера входных данных. Проще говоря: если вы увеличите n в 10 раз, время работы (в худшем приближении) вырастет примерно в 10? = 100 раз. Такие алгоритмы быстро становятся непрактичными при росте объёма данных — поэтому важно уметь их распознавать, оценивать и по возможности заменять.
Приведённый ниже пример демонстрирует работу алгоритма пузырьковой сортировки массива Как работает пузырьковая сортировка:
Копировать в буфер обмена
метод Скрипт() КвадратичнаяCложность() ; метод КвадратичнаяCложность() знч Массив100 = ПолучитьМассивСлучайныхЧисел(100) знч Массив1000 = ПолучитьМассивСлучайныхЧисел(1000) пер НачалоОперации = ДатаВремя.Сейчас() пер КоличествоИтераций = СортировкаПузырьком(Массив100) пер ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время сортировки массива 100 элементов: %{ДлительностьОперации} мс. Количество итераций: %{КоличествоИтераций}") НачалоОперации = ДатаВремя.Сейчас() КоличествоИтераций = СортировкаПузырьком(Массив1000) ДлительностьОперации = (ДатаВремя.Сейчас() - НачалоОперации).ВМиллисекундах() Консоль.Записать("Время сортировки массива 1000 элементов: %{ДлительностьОперации} мс. Количество итераций: %{КоличествоИтераций}") ; метод СортировкаПузырьком(ИсходныйМассив: Массив<Число>): Число пер ДлинаМассива = ИсходныйМассив.Граница() пер КоличествоИтераций = 0 для i = 0 по ДлинаМассива - 1 // Внутренний цикл: до (n - 1 - i), потому что конец уже отсортирован для j = 0 по (ДлинаМассива - 1 - i) КоличествоИтераций += 1 если (ИсходныйМассив[j] > ИсходныйМассив[j + 1]) // Меняем элементы местами (деструктуризация) знч temp = ИсходныйМассив[j] ИсходныйМассив[j] = ИсходныйМассив[j + 1] ИсходныйМассив[j + 1] = temp ; ; ; Консоль.Записать(ИсходныйМассив.Представление().Обрезать(100, "...")) возврат КоличествоИтераций ;
Результат выполнения:
Время сортировки массива 100 элементов: 15 мс. Количество итераций: 4950
Время сортировки массива 1000 элементов: 301 мс. Количество итераций: 499500
Во вложенных циклах (внешний индекс i, внутренний j) внутренняя итерация выполняется n - i - 1 раз при каждом i. Общее число итераций (парных сравнений) равно сумме
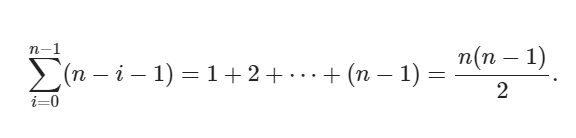
Посчитаем для n:
Отношение количества итераций:
499500/4950 = 100,90
То есть при увеличении n в 10 раз число сравнений выросло примерно в ~101 раз — близко к ожидаемому квадратичному росту (?100?).
Мы наблюдаем: 15 ? 301 мс, то есть время выросло в ~20 раз (301/15 = 20,06):
Это не противоречит асимптотике — O(n?) описывает поведение при больших n, но не гарантирует точной кратности времени числу итераций. Причины рассогласования:
Итог: итерации показывают идею роста (~n?), а время — реальное поведение, где константы и оборудование решают, насколько близко результаты к этой теоретической кривой.
Типичные свойства пузырьковой сортировки и O(n?)
Экспоненциальная сложность — одна из самых «болезненных» для практики: время выполнения растёт вдвое с добавлением каждого нового элемента. Такие алгоритмы встречаются в задачах перебора всех комбинаций/подмножеств, в наивных решениях задач комбинаторики и во многих NP-трудных задачах.
Приведённый ниже пример демонстрирует работу полного перебора всех подмножеств множества из n элементов:
Копировать в буфер обменаметод Скрипт() ЭкспоненциальнаяСложность() ; метод ЭкспоненциальнаяСложность() для РазмерМассива = 5 по 20 шаг 5 Консоль.Записать("Элементов: $РазмерМассива, вызовов: ${ПодсчётПодмножеств(РазмерМассива)}") ; ; метод Перебор(индекс: Число, всего: Число, Счётчик: Массив<Число>) Счётчик[0] += 1 если (индекс == всего) возврат ; Перебор(индекс + 1, всего, Счётчик) // без текущего элемента Перебор(индекс + 1, всего, Счётчик) // с текущим элементом ; метод ПодсчётПодмножеств(РазмерМассива: Число): Число пер Счётчик = [0] Перебор(0, РазмерМассива, Счётчик) возврат Счётчик[0] ;
Результат:
Элементов: 5, вызовов: 63
Элементов: 10, вызовов: 2 047
Элементов: 15, вызовов: 65 535
Элементов: 20, вызовов: 2 097 151
Что делает этот код и почему рост — экспоненциальный
Это и даёт числа: для n = 5 ? , для n = 10 ? и т. д.
Заметьте: количество подмножеств равно (2^n) (это число листьев), но количество вызовов функции — немного больше, потому что в дереве есть внутренние узлы: всего
Характер роста — «каждый новый элемент удваивает объём работы»
Ключевое свойство экспоненциальной сложности: если вы добавите один элемент, число вызовов примерно удвоится. Это делает алгоритмы экспоненциального класса быстро непрактичными:
Чтобы дать интуитивное представление: если одна рекурсивная «штука» занимает 1 микроcекунду, то n=20 ? 2 с, n=30 ? 2 147 с (~36 мин), n=50 ? 2,25·10? с (~71 год). Даже при 100 нс на вызов n=50 даёт многие годы.
Где такие алгоритмы появляются на практике
Практические последствия и рекомендации инженеру
Экспоненциальная сложность — это красная зона алгоритмической эффективности.
Каждое добавление нового элемента почти удваивает объём вычислений, и даже при малых входных данных время быстро выходит за разумные пределы.
Такие алгоритмы допустимы только для очень небольших n или в задачах, где других решений нет (например, при полном переборе комбинаций).
Главное — распознавать экспоненциальный рост и не допускать его в код реальных проектов без строгих ограничений по входным данным.
Разработчик не боится экспоненты — он понимает, когда её можно себе позволить, а когда нужно искать иной путь.
Факториальная сложность — это крайняя точка роста вычислительных затрат: количество операций (и часто — объём памяти) растёт как факториал от размера входа. На практике это означает, что каждое увеличение n на единицу умножает количество возможных вариантов на n — и потому даже при небольших n перебор становится быстро невыполнимым. Приведённый ниже пример демонстрирует генерацию всех перестановок элементов массива:
Копировать в буфер обменаметод Скрипт() ФакториальнаяСложность() ; метод ФакториальнаяСложность() для РазмерМассива = 2 по 8 шаг 2 знч ИсходныйМассив = ПолучитьМассивСлучайныхЧисел(РазмерМассива) знч МассивРезультаты = Перестановки(ИсходныйМассив) Консоль.Записать("Количество перестановок: ${МассивРезультаты.Размер()}") ; ; // Метод перебора перестановок метод ПереборПерестановок(ТекущаяРасстановка: Массив<Число>, Оставшиеся: Массив<Число>, Результат: Массив<Строка>) если Оставшиеся.Пусто() // Преобразуем текущую перестановку в строку через запятую и добавляем в результат Результат.Добавить(ТекущаяРасстановка.Представление()) возврат ; для Индекс = 0 по Оставшиеся.Размер() - 1 знч Элемент = Оставшиеся[Индекс] // Создаём новую текущую перестановку знч НоваяТекущая = <Число>[] НоваяТекущая.ДобавитьВсе(ТекущаяРасстановка) НоваяТекущая.Добавить(Элемент) // Создаём массив оставшихся без текущего элемента знч НовыеОставшиеся = <Число>[] для i = 0 по Оставшиеся.Размер() - 1 если i != Индекс НовыеОставшиеся.Добавить(Оставшиеся[i]) ; ; // Рекурсивный вызов ПереборПерестановок(НоваяТекущая, НовыеОставшиеся, Результат) ; ; // Метод генерации всех перестановок метод Перестановки(ИсходныйМассив: Массив<Число>): Массив<Строка> знч Результат = <Строка>[] ПереборПерестановок(новый Массив<Число>(), ИсходныйМассив, Результат) возврат Результат ;
Результат:
Количество перестановок: 2
Количество перестановок: 24
Количество перестановок: 720
Количество перестановок: 40 320
Что здесь происходит и почему n!
Алгоритм генерирует все перестановки входного массива. На каждом уровне рекурсии выбирается один из оставшихся элементов для следующей позиции, после чего остаётся задача той же природы, но с на один элемент меньшим набором. Таких полных упорядоченных размещений ровно n! — факториал n:
Для примеров выше это даёт:
Именно эти числа отображены в вывода программы.
Анализ сложности (временная и пространственная)
Факториал очень быстро выходит за рамки практического времени и памяти. Для наглядности:
Даже если затраты на одну перестановку малы, факториал «съедает» любую оптимизацию констант.
Алгоритмы со сложностью O(n!) появляются, когда нужно перебрать все возможные порядки или комбинации элементов. Например:
Генерация всех перестановок — естественная и иногда необходимая операция, но асимптотически это O(n!), а фактические затраты часто оцениваются как ?(n · n!) при создании/сохранении каждой перестановки. Факториал растёт невероятно быстро: то, что выполнимо для n = 8, становится невозможным для n = 15 и практически немыслимо для n = 20.
Практическое правило: распознавать признаки факториальной сложности и по возможности избегать полного перебора. Если же полный перебор неизбежен, следует явно фиксировать допустимый максимум n, проектировать потоковую обработку (чтобы не хранить всё в памяти) и документировать ожидаемые ресурсы — это помогает принимать инженерные решения заранее, а не сталкиваться с неожиданным «взрывом» затрат в продакшне.
Анализ сложности алгоритмов — это не абстрактная теория, а инструмент практического мышления разработчика. Он позволяет видеть не просто, как работает код сейчас, но и как он будет вести себя в будущем, когда объём данных или нагрузка системы увеличатся.
Понимание временной и пространственной сложности (O(n), O(n log n), O(n?) и других классов) даёт возможность предсказывать потенциальные узкие места ещё до появления первых проблем. Это особенно важно в системах, где масштабируемость и производительность критичны: от веб-приложений до алгоритмов машинного обучения и планирования маршрутов.
Хороший инженер не просто избегает сложных алгоритмов, а умеет оценить компромиссы между скоростью, использованием памяти и простотой реализации. Иногда линейный алгоритм уступает в скорости, но экономит память; иногда эвристика или приближённый метод оказывается более разумным выбором, чем точное решение NP-трудной задачи.
Асимптотический анализ — это язык, на котором эти компромиссы выражаются формально и объективно. Он помогает:
В конечном счёте, зрелость разработчика проявляется не только в написании работающего кода, но и в умении предвидеть его пределы, понимать масштабируемость и рационально управлять сложностью.
Анализ алгоритмов — это неразрывная часть инженерной культуры, инструмент, который превращает написание кода в осознанное проектирование решений, готовых к росту и изменениям.